高温銅酸化物超伝導体における面外歪みによる酸素同位体効果の増大について
- タイトル: 高温銅酸化物超伝導体における面外歪みによる酸素同位体効果の増大について
- 論文:Physical Review B 80, 212501 (2009).
- 著者:K. Sato, H. Iwasawa, N. C. Plumb, T. Masui, Y. Yoshida, H. Eisaki, H. Bando, A. Ino, M. Arita, K. Shimada, H. Namatame, M. Taniguchi, S. Tajima, Y. Nishihara, D. S. Dessau, and Y. Aiura
- 機関:産業技術綜合研究所、茨城大学、コロラド大学、大阪大学、広島大学大学院理学研究科、広島大学放射光化学研究センター
超伝導は物質の電気抵抗率がある温度(超伝導転移温度TC)以下で完全にゼロになる現象です。超伝導の基本的なメカニズムについては、1957年にバーディーン、クーパー、シュリファーの3人によって解明されました(BCS理論)。BCS理論によると超伝導物質を構成している原子核格子の振動(フォノン)が媒介して、通常は反発しあう電子と電子の間に引力がはたらき(電子フォノン相互作用)、TC以下で電子の束縛状態(クーパー対)が形成されて超伝導状態が生じます。BCS理論によると原子核が重くなると格子振動の周波数が低下し、TCが下がります。実際に原子番号が同じで、原子核の重さが異なる同位体を用いて実験すると、同位体が重くなるほどTCが下がることが明らかになりました(同位体効果)。
銅系高温超伝導体もまた発見された直後から、電子フォノン相互作用が高温超伝導のメカニズムに密接に関与しているのではないかと考えられ、数多くの同位体効果に関する研究が行われてきました。銅系高温超伝導体のTCは電気伝導をになうキャリア濃度に依存しており、TCが最大となるキャリア濃度を最適ドープ、それよりも低い濃度を不足ドープ、高い濃度を過剰ドープと呼びます。不足ドープ領域側では同位体置換による大きな超伝導転移温度の低下が見られました。ところが最適~過剰ドープ領域側ではわずかの同位体効果しか示されず、BCS理論から予想されるふるまいとは異なりました。これまでの実験結果により、高温超伝導の起源はフォノン以外の「何か」がクーパー対形成に働いているのではないかという主張もなされるようになりました。
超伝導に転移すると、超伝導状態は常伝導状態(超伝導でない状態)にくらべてエネルギーが低くなります。そのエネルギー差を超伝導ギャップと言います。これまで知られてきた金属超伝導体と異なり、銅系高温超伝導体には超伝導に転移する温度よりもはるかに高い温度から、超伝導状態に類似した電子状態が観測され、エネルギーギャップ(擬ギャップ)が存在していることが分かりました。現在、高温超伝導の振る舞いを解明するうえで超伝導ギャップと擬ギャップの相互の関係を理解することが重要であると考えられています。そこで、私たちはこれまで報告された銅系高温超伝導体の「特異な」酸素同位体効果の解釈するために、これら2つのギャップに対する酸素同位体効果の解明に取り組みました。
私たちはキャリア数を同じにし、結晶歪みだけを制御した銅系高温超伝導体試料Bi2Sr1.6Ln0.4CuO6+δ を用いて酸素同位体効果の研究を行いました。結晶歪みは、この物質に含まれるランタノイド元素(Ln)をLaからGdまで系統的に変化させることにより制御できます。すなわちランタノイド元素をLaからGdに変えて行くとイオン半径が小さくなるため(「ランタノイド収縮」と呼ばれます)、結晶の歪みが増加していきます。
HiSOR BL-9Aの低エネルギー高分解能角度分解光電子分光により、キャリア数が一定であることが精密に評価でき、これが本研究で大変重要なことでした。つまり、以下に示す酸素同位体効果は、キャリア数の変化に引き起こされるのではなく、結晶歪によることを確認できました。ランタノイド置換による結晶歪みは、超伝導ギャップサイズを変化させず、擬ギャップサイズだけを変えることが分かっています。超伝導転移温度(TC)の酸素同位体効果を調べた結果を図1に示します。結晶歪みの増加とともにTCが急激に減少しますが、酸素同位体置換に伴う転移温度の減少(ΔTC)はほぼ一定です(図1(a))。その結果、αTC≡-d ln(TC)/d ln(M)で与えられるTCの酸素同位体シフト量は、結晶歪みの増加(すなわち ランタノイド置換によるTCの減少)に伴い、急激に増加することが明らかになりました(図1(b))。
この酸素同位体効果の結果は、「超伝導ギャップの酸素同位体効果は存在するが、擬ギャップの酸素同位体効果は存在しない」というモデルにより定量的に解釈できることが示されました(図1(c))。古くから知られている金属超伝導体も同様のモデルで解釈できます。ただし金属超伝導体は擬ギャップが存在しないので、超伝導ギャップと超伝導転移温度が直接関係しています。
今回の実験結果は、同位体効果は超伝導転移温度や擬ギャップでなく超伝導ギャップに直接関係していることを示唆しています。超伝導ギャップと擬ギャップで酸素同位体効果が異なることを明らかにしたことは、今後の超伝導の起源の解明、特に電子フォノン相互作用の役割を解明する上で重要な知見を与えました。
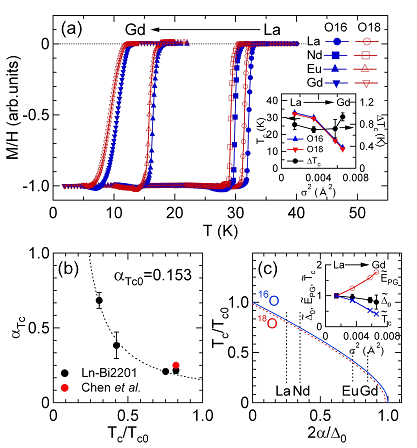
図1 銅系高温超伝導体の超伝導転移温度の酸素同位体シフトの結晶歪効果
米国物理学会
https://journals.aps.org/prb/abstract/10.1103/PhysRevB.80.212501











